The CubicSurfaceExtractor creates a mesh in which each voxel appears to be rendered as a cube. More...
#include <CubicSurfaceExtractor.h>
Classes | |
| struct | IndexAndMaterial |
| struct | Quad |
Public Member Functions | |
| CubicSurfaceExtractor (VolumeType *volData, Region region, SurfaceMesh< PositionMaterial > *result, bool bMergeQuads=true, IsQuadNeeded isQuadNeeded=IsQuadNeeded()) | |
| void | execute () |
Detailed Description
template<typename VolumeType, typename IsQuadNeeded = DefaultIsQuadNeeded<typename VolumeType::VoxelType>>
class PolyVox::CubicSurfaceExtractor< VolumeType, IsQuadNeeded >
The CubicSurfaceExtractor creates a mesh in which each voxel appears to be rendered as a cube.
Introduction
Games such as Minecraft and Voxatron have a unique graphical style in which each voxel in the world appears to be rendered as a single cube. Actually rendering a cube for each voxel would be very expensive, but in practice the only faces which need to be drawn are those which lie on the boundary between solid and empty voxels. The CubicSurfaceExtractor can be used to create such a mesh from PolyVox volume data. As an example, images from Minecraft and Voxatron are shown below:
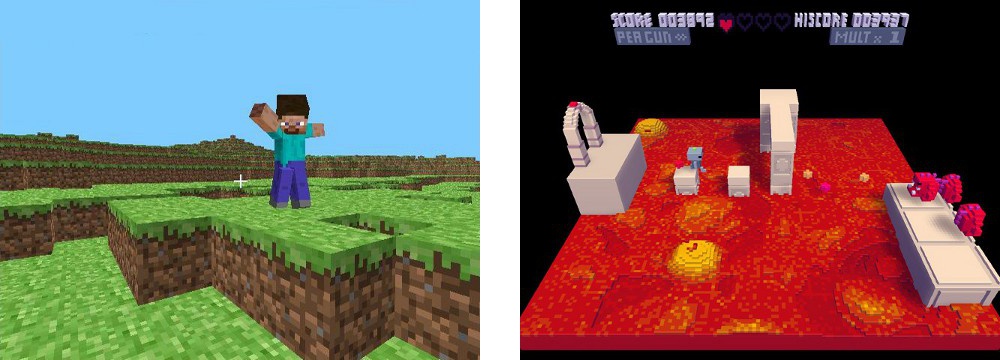
Before we get into the specifics of the CubicSurfaceExtractor, it is useful to understand the principles which apply to all PolyVox surface extractors and which are described in the Surface Extraction document (ADD LINK). From here on, it is assumed that you are familier with PolyVox regions and how they are used to limit surface extraction to a particular part of the volume. The principles of allowing dynamic terrain are also common to all surface extractors and are described here (ADD LINK).
Basic Operation
At its core, the CubicSurfaceExtractor works by by looking at pairs of adjacent voxels and determining whether a quad should be placed between then. The most simple situation to imagine is a binary volume where every voxel is either solid or empty. In this case a quad should be generated whenever a solid voxel is next to an empty voxel as this represents part of the surface of the solid object. There is no need to generate a quad between two solid voxels (this quad would never be seen as it is inside the object) and there is no need to generate a quad between two empty voxels (there is no object here). PolyVox allows the principle to be extended far beyond such simple binary volumes but they provide a useful starting point for understanding how the algorithm works.
As an example, lets consider the part of a volume shown below. We are going to explain the principles in only two dimensions as this makes it much simpler to illustrate, so you will need to mentally extend the process into the third dimension. Hopefully you will find this intuitive. The diagram below shows a small part of a larger volume (as indicated by the voxel coordinates on the axes) which contains only solid and empty voxels represented by solid and hollow circles respectively. The region on which we are running the surface extractor is marked in pink, and for the purpose of this example it corresponds to the whole of the diagram.
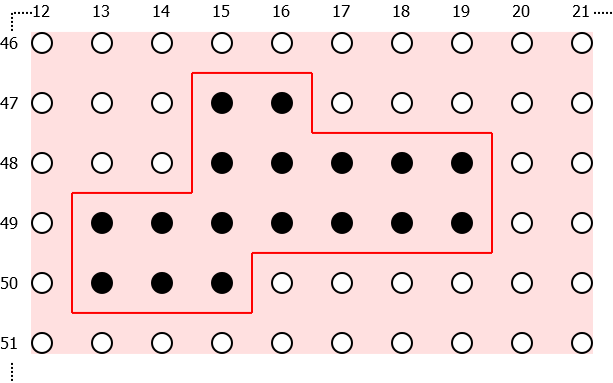
The output of the surface extractor is the mesh marked in red. As you can see, this forms a closed object which corrsponds to the shape of the underlying voxel data. We won't describe the rendering of such meshes here - for details of this please see (SOME LINK HERE).
Working with Regions
So far the behaviour is easy to understand, but let's look at what happens when the extraction is limited to a particular region of the volume. The figure below shows the same data set as the previous figure, but the extraction region (still marked in pink) has been limited to 13 to 16 in x and 47 to 51 in y:
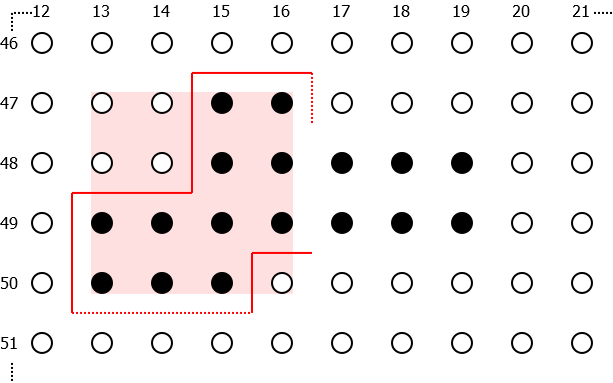
As you can see, the extractor continues to generate a number of quads as indicated by the solid red lines. However, you can also see that the shape is no longer closed. This is because the solid voxels actually extend outside the region which is being processed, and so the extractor does not encounter a boundary between solid and empty voxels. Although this may initially appear problematic, the hole in the mesh does not actually matter because it will be hidden by the mesh corresponding to the region adjacent to it (see next diagram).
More interestingly, the diagram also contains a couple of dotted red lines lying on the bottom and right hand side of the extracted region. These are present to illustrate a common point of confusion, which is that no quads are generated at this position even though it is a boundary between solid and empty voxels. This is indeed somewhat counter intuitive but there is a rational reasaoning behind it. If you consider the dashed line on the righthand side of the extracted region, then it is clear that this lies on a boundary between solid and empty voxels and so we do need to create quads here. But what is not so clear is whether these quads should be assigned to the mesh which corresponds to the region in pink, or whether they should be assigned to the region to the right of it which is marked in blue in the diagram below:
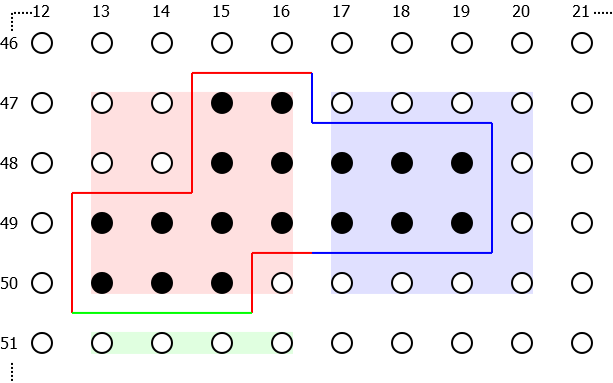
We could choose to add the quads to both regions, but this can cause confusion when one of the region is modified (causing the face to disappear or a new one to be created) as both regions need to have their mesh regenerated to correctly represent the new state of the volume data. Such pairs of coplanar quads can also cause problems with physics engines, and may prevent transparent block from rendering correctly. Therefore we choose to instead only add the quad to one of the the regions and we always choose the one with the greater coordinate value in the direction in which they differ. In the above example the regions differ by the 'x' component of their position, and so the quad is added to the region with the greater 'x' value (the one marked in blue).
Note: This behaviour has changed recently (September 2012). Earlier versions of PolyVox tried to be smart about this problem by looking beyond the region which was being processed, but this complicated the code and didn't work very well. Ultimatly we decided to simply stick with the convention outlined above.
One of the practical implications of this is that when you modify a voxel you may have to re-extract the mesh for regions other than region which actually contains the voxel you modified. This happens when the voxel lies on the upper x,y or z face of a region. Assuming that you have some management code which can mark a region as needing re-extraction when a voxel changes, you should probably extend this to mark the regions of neighbouring voxels as invalid (this will have no effect when the voxel is well within a region, but will mark the neighbouring region as needing an update if the voxel lies on a region face).
Another scenario which sometimes results in confusion is when you wish to extract a region which corresponds to the whole volume, partcularly when solid voxels extend right to the edge of the volume.
Definition at line 77 of file CubicSurfaceExtractor.h.
Constructor & Destructor Documentation
| PolyVox::CubicSurfaceExtractor< VolumeType, IsQuadNeeded >::CubicSurfaceExtractor | ( | VolumeType * | volData, |
| Region | region, | ||
| SurfaceMesh< PositionMaterial > * | result, | ||
| bool | bMergeQuads = true, |
||
| IsQuadNeeded | isQuadNeeded = IsQuadNeeded() |
||
| ) |
Definition at line 38 of file CubicSurfaceExtractor.inl.
Member Function Documentation
| void PolyVox::CubicSurfaceExtractor< VolumeType, IsQuadNeeded >::execute | ( | ) |
Definition at line 48 of file CubicSurfaceExtractor.inl.
The documentation for this class was generated from the following files:
- PolyVoxCore/include/PolyVoxCore/CubicSurfaceExtractor.h
- PolyVoxCore/include/PolyVoxCore/CubicSurfaceExtractor.inl
 1.8.1
1.8.1